Non-line-of-sight Imaging

(a) typical NLOS imaging setup (b) Top:Fourier spectrum of different kernels. Bottom: Recovered depths using different kernels.

Abstract:

Recovering information from non-line-of-sight (NLOS) imaging is a computationally-intensive inverse problem. Most physics-based NLOS imaging methods address the complexity of the problem by assuming three-bounce reflections and no self-occlusion. However, these assumptions may break down for objects with large depth variations, preventing physics-based algorithms from accurately reconstructing the details and high-frequency information. On the other hand, while learning-based methods can avoid these assumptions, they may struggle to reconstruct details without specific designs due to the spectral bias of neural networks. To overcome these issues, we propose a novel approach that enhances physics-based NLOS imaging methods by introducing a learnable inverse kernel in the Fourier domain and using an attention mechanism to improve the neural network’s ability to learn high-frequency information. Our method is evaluated on synthetic datasets that we create and that are publicly available, demonstrating its superior performance compared to prior physics-based and learning-based methods, especially for objects with large depth variations. Moreover, our approach generalizes well to real data and can be applied to tasks such as classification and depth reconstruction.

Attention-guided kernel learning

Pipeline

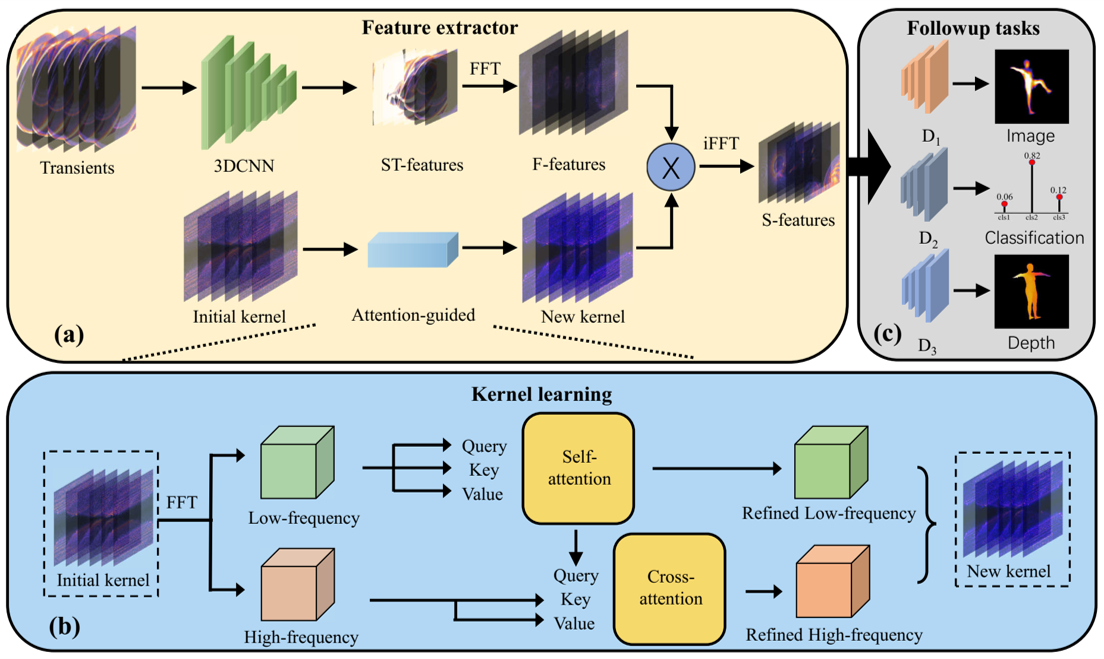
Overview of our framework. In the top row we illustrate our framework. Our framework first takes as input a raw transient and output a downsample feature volume (S-T features) with a 3D CNN. Then we map the feature volume into a Fourier space so as to convolve with our learned kernel $\mathcal{K}$, yielding spatial features (S-feature) that suits followup tasks. In the bottom row, we show how we learn our kernel. Our kernel is implemented as a learnable Fourier volume that is initialized with LCT. We then conduct our proposed attention guidance learning to enhance the $\mathcal{K}$ for light cone transform in the deep Fourier space.

The code and dataset is available at Code Release.